Ik kom even ongegeneerd spammen hier. Zouden jullie alsjeblieft de survey in willen vullen voor mijn master thesis? Het is in het Engels en minder dan 5 minuten werk gelukkig! Ik heb echt nog behoorlijk wat respondenten nodig 
https://uvacommscience.eu.qualtrics.com/jfe/form/SV_ekw7XQwUcEnQ8sd
Heb hem voor je ingevuld!
Ingevuld. Succes!
Sorry als het al eens gevraagd is, maar ik kon het zelf niet vinden hier: gebruiken jullie browser-extensies om je bibliografie bij te houden (voor essays/scriptie)? Zo ja, welke is het fijnst? Ik begin binnenkort aan mijn scriptie en heb begrepen dat zo iets wel handig is.
Ik doe het gewoon zelf typen in word. Ik merk dat er te vaak fouten in sluipen met zulke programma’s en dan ben je evenveel tijd kwijt met dat controleren en bewerken.
Zotero (open source)!
(Mocht het je wat doen: Mendeley is overgenomen door Elsevier in 2013 (en Elsevier probeer ik te mijden. Hier een interessant esay over Elsevier)) .
Nog een vraagje! Hoe controleren jullie je spelling etc. bij Engelse teksten? Ik gebruik voor Nederlandse teksten altijd spelcheck.nl, vind het fijn om het nog even extra te controleren. Nu zoek ik iets soortgelijks maar dan in het Engels. Heb wel een aantal websites gevonden maar die doen het echt per woord, en dat werkt niet heel lekker.
Toevallig hier iemand die veel weet over moderatie? Ik ben een theoretisch kader aan het schrijven en vraag mij af of je in het theoretisch kader ook de relatie van de X tot de MOD moet aantonen of alleen van de Y tot de MOD. Het lijkt me logisch dat je beiden moet doen, maar begin door andere studies beetje te twijfelen 
Jazeker, al begrijp ik je vraag niet helemaal. Je hebt het namelijk over de relatie van X op Z (moderatie-variabele) en Y op Z. Dan zou je dus dit krijgen:
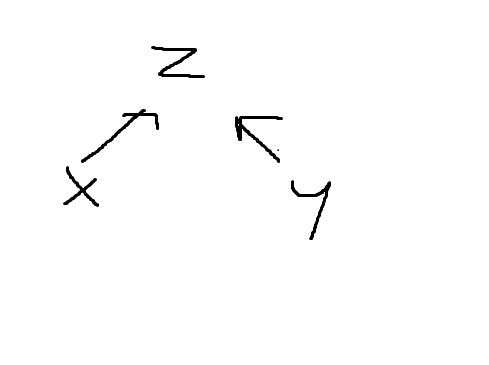
Waarbij de variabele die je wil verklaren dus eigenlijk Z is, en de predictors die je gebruikt X en Y.
Een moderatie, of interactie, betekent dat het EFFECT van X op Y verschilt voor verschillende levels van je moderatie-variabele. Wat in mijn veld normaal is, is om eerst het directe effect van X op Y te beschrijven en je hypothese te beschrijven. Daarna beschrijf je welke variabele de moderatie-variabele is, wat het mechanisme is en wat voor’n verschil in de relatie van X op Y je dan verwacht (dus ook een hypothese voor dit stuk).
Voorbeeld: het effect van aantal auto’s op blijdschap (X op Y). Dan leg je in je theoriestuk dit eerst uit. Dan verwacht je op basis van theorie, dat deze relatie (van X op Y) verschilt voor mannen en vrouwen (bv. voor mannen is het effect sterker dan voor vrouwen). In andere woorden: het effect van 1 auto extra hebben op blijdschap is groter/sterker voor mannen. Het heeft dus niks te maken of mannen en vrouwen meer auto’s hebben, maar dus of het EFFECT van X op Y verschilt voor mannen vrouwen (vaak gaat het dan er om dat het voor een bepaalde groep sterker of zwakker is).
De twee hypothesen van het voorbeeld zouden dan zijn (en let niet op de verwoording, ff snel bedacht):
H1: De meer auto’s iemand heeft, de blijer iemand is
H2: Het effect van het aantal auto’s op blijdschap is sterker voor mannen dan voor vrouwen.
Schematisch zou het een interactie-effect er dan zo uit zien:
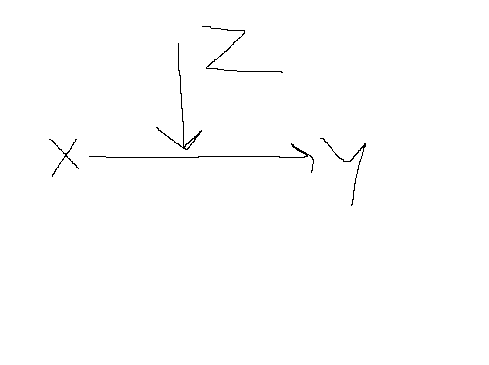
(Kleine side note: ik verwacht dus een linear effect van X op Y in dit voorbeeld)
(Tweede kleine side note: mijn tekeningen zijn lelijk lol
Iemand die ik ken gebruikt Grammarly (zelf geen ervaring mee), en die is erg tevreden.
Meka, DANK JE WEL. Je hebt mij de vorige keer ook zo goed geholpen met een statistisch probleem. Ik had het een beetje warrig verwoord; ik bedoelde inderdaad de rol van de MOD op de relatie tussen x en y.
Ik zit er alleen mee dat ik geen categorische MOD heb (zoals sekse), maar een ordinale/scale MOD. Afgaande op jou voorbeeld zou dit bijvoorbeeld ‘mate van aantrekkelijkheid van de autobezitter’ zijn waardoor ik het een beetje moeilijk vind verwoorden.
Dus het effect van een 1 extra auto op blijdschap is groter/sterker bij een hoge mate van aantrekkelijkheid? En is het automatisch zo dat een MOD twee kanten op werkt: het effect van 1 extra auto is lager/zwakker bij een lage mate van aantrekkelijkheid?
Dus als ik het goed begrijp zou onderstaande de beste opbouw voor mijn theoretisch kader zijn?
Yw!
Wat zijn je variabelen (en wat is de operationalisatie/hoe zijn ze gemeten [is het een schaal bv])? Het maakt het nu complex om te vertellen hoe je het het beste zou doen zonder te weten wat je X, Y en Z zijn 
Vind je het goed als ik je er een priveberichtje over stuur (ivm herkenbaarheid)?
Dank je alvast!! 
(de stress voor de kerst is groot haha)
Ja, is goed!
Ik dacht dat er een scriptie topic was maar ik kan hem nergens vinden dus ik stel mijn vraag hier even. Ik doe een tevredenheidsonderzoek bij een bedrijf met ± 140 werknemers. Nu had ik helemaal een steekproef berekend en deze kwam uit op 103 personen, maar nu gaf mijn begeleider de terechte feedback dat het meer op een censusonderzoek lijkt en dat is eigenlijk ook zo want ik wil de enquete verspreiden onder alle medewerkers. Alleen de kans dat niet iedereen reageert en ik dus geen 140 ingevulde enquetes heb is erg groot (er zijn bijv ook medewerkers die bijna niet meer werken of die weinig van zich laten horen). Hoe verwerk ik dit in het onderzoek? En hoe zit het dan met de betrouwbaarheid etc?
Ja dat was ook het idee inderdaad! Alleen ik heb in de methodologie beschreven hoe de steekproef is berekend maar bij een censusonderzoek is een steekproef niet nodig (dit is de feedback van mijn begeleider) omdat je alle medewerkers ondervraagt. Dus dan kan de hele steekproefberekening eruit denk ik? Maar is het onderzoek dan wel betrouwbaar als niet alle medewerkers het invullen of is er dan ook een minimaal aantal respondenten?
Alleen in een ideale wereld bereik je 100% van de respondenten. Ik zou ze sowieso een of twee reminders sturen en eventueel een bon verloten. Ik denk dat je met 75% al behoorlijk betrouwbaar zit? Maar pin me daar niet op vast.
Je moet vooral kunnen verantwoorden of je uiteindelijke steekproef nog representatief is voor de gehele populatie. Dus stel er zijn 140 medewerkers waar 30 vrouwen werken en 110 mannen en uiteindelijk heb je 110 respondenten waarvan 108 man dan is je steekproef niet meer representatief en mag je geen uitspraken doen over het gehele bedrijf. Hetzelfde geldt bijvoorbeeld als blijkt dat alle parttime medewerkers de vragenlijst niet invullen etc. Dus ik zou goed bijhouden wie wel/niet de vragenlijst invult en voor bepaalde factoren die belangrijk zijn voor je onderzoek verantwoorden of hier geen systematiek in zit. Daarbij zou ik idd altijd streven naar een zo groot mogelijke n dus reminder sturen en dat proces goed beschrijven.
Die baankansen van de uni vertrouw ik niet helemaal eerlijk gezegd :"P. Ik zie zelf namelijk bij mijn eerste master dat de baankans vrij hoog was, maar vrij weinig mensen hebben nu (sinds juni dus) een baan. Edit: dit komt bijvoorbeeld omdat een aantal mensen door gaan studeren omdat ze geen baan konden vinden en niet worden meegenomen in de statistieken.
Ik doe nu ook een tweede master. Mijn eerste master was een eenjarige, dit is een tweejarige (Ik had ook al wat vertraging omdat ik eerst twee jaar hbo had gedaan en toen een universitaire bachelor ben gaan doen). Vind je de tweede master even leuk/interessant en heeft die master naar jouw idee wel betere baankansen?
En sowieso: ik merk in mijn omgeving dat als je bijvoorbeeld cum laude slaagt en/of veel nevenactiviteiten hebt gedaan, het ook veel makkelijker is om een baan te vinden. Zelfs als de baankansen lager zijn. Ik weet niet of het haalbaar is voor jou, maar mocht je voor de master kiezen met een lagere baankans, dan zou ik zeker proberen je te onderscheiden van anderen.
En nog ff een persoonlijk iets: ik ben oprecht zo blij dat ik twee master doe en ik raad het iedereen aan! De eerste master bleek al vrij snel niet interessant/te makkelijk, maar ik heb wel een jaar extra gehad om na te denken wat ik hierna wilde doen/mijn cv uit te breiden. Ik zou persoonlijk wel twee masters kiezen die verschillen.
Ik weet niet waar je wil studeren, maar de uni betaald bij mij het verschil tussen collegegeld en instellingsgeld.
De UU heeft hiervoor een regeling:
‘’ Heb je in 2017-2018 of 2018-2019 een masterdiploma behaald aan de UU (tegen het wettelijk tarief) en ga je aansluitend, in studiejaar 2018-2019, een masteropleiding aan de UU volgen, dan betaal je in 2018-2019 het instellingstarief ter hoogte van het wettelijk tarief, zolang je de tweede master niet onderbreekt."
Dan zou ik zeker voor de eerste master gaan :)!
Mocht je nou achteraf echt spijt hebben (wat waarschijnlijk niet het geval gaat zijn), dan kan je er altijd nog voor kiezen om verder te gaan studeren (misschien wil je werkgever dat betalen of kan je in een goedkoper land een master doen; genoeg opties mogelijk).